Tuning and Temperament
A (very) abbreviated history of
tuning theory, 550 BCE - 2006 CEBy Paul Guy © Paul Guy 1999 - 2006
Pythagoras
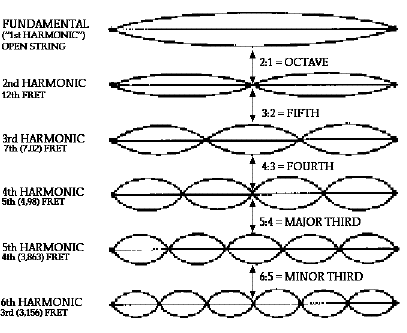
The Harmonic Series
The Harmonists
Just Intonation
Meantone Intonation
Well Temper
The Well-Tempered Clavier
Fretted Instruments
Equal TemperamentAll tuning is ultimately based on the harmonic series, which arises from the physical behaviour of vibrating strings. A vibrating string produces a whole spectrum of related frequencies. (See Fig. 1.) The fundamental, or first harmonic, is the frequency at which the overall speaking length of a string vibrates. The overtones are the frequencies of the string’s higher vibrational modes - the second harmonic (one octave above the fundamental) is produced by a pattern of two separately vibrating ”loops”, each one-half of the speaking length. The third harmonic (an octave and a fifth above the fundamental) is produced by a pattern of three ”loops”, each one-third of the speaking length. The fourth harmonic (two octaves above the fundamental) is produced by four loops each one-quarter of the speaking length and the fifth harmonic (two octaves and a major third) by five loops each one-fifth of the spaeking length, and the sixth harmonic (two octaves and a fifth) by six loops... and so on. Guitarists are familiar with these fractions of the string length as the locations of natural harmonics. This concept is vital to the understanding of why we tune musical instruments the way we do.
Fig. 1: The harmonic series
Pythagoras
No other single figure in written history has had more influence on the tuning of musical instruments than Pythagoras, the ancient Greek mathematician, philosopher, and mystic, known to every schoolchild for his theorem - "in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides".
Images of childhood geometry lessons notwithstanding, Pythagoras was no dusty, boring academic - he was a flamboyant, charismatic sage, who dressed in white robes and wore a gold coronet. One of the great geniuses of antiquity, Pythagoras was born on the Greek island of Samos in about 580 BCE. Leaving Samos at age 18, he studied in Egypt for 22 years and in Babylon for a further 12 years, collecting the accumulated mathematical knowledge of these ancient lands, and becoming initiated into the mystery religions of their peoples. (He visited many other countries along the way - some claim he even travelled as far as India.) When he finally returned to Samos, burning with enthusiasm to found a centre of learning, he found that it had become a narrow-minded, intolerant society with no place for his new-fangled ideas. He was offered a place at court, but as he realised that this was just a ploy to keep him quiet, he elected instead to live in a cave in an isolated part of the island.
Pythagoras was ultimately forced to flee Samos with his mother and his sole student and settled in Crotona, a Greek colony in southern Italy, in about 530 BCE, where (at age 56) he founded a philosophical, religious, and political society called "The Pythagorean Brotherhood", which was to have a profound influence on Socrates, Plato and other later "thinkers". Pythagoras is often called the "founder" of philosophy, in that he is said to have coined the very term "philosopher", when asked to describe himself. It means, roughly, "lover of wisdom".
He taught that the earth was a rotating sphere, orbiting the "central fire" of the sun in company with the six other (then known) planets. He believed that the orbiting planets each produced a different musical note, and that the ratios of the planets' orbital distances defined the pitches. The resulting chord made a "Music of the Spheres" too ethereal for uninitiated human ears to hear. Pythagoras claimed to be able to hear this music, and would sing the tunes to his disciples!
Pythagoras left no writings of his own; all that is known of his teachings comes from his followers. He was murdered, some say on the orders of a piqued potentate who had been refused entry to the Brotherhood, in about 500 BCE.
The Pythagorean scalePythagoras' enquiring mind led him to investigate the physical properties of vibrating strings. The lyres and kitharas (lap harps) of ancient Greece had four strings until around 650 BCE, when - according to legend - the musician and poet Terpander, the "Father of Greek music" is said to have improved them by increasing the number of strings to 7.
About a century after that Pythagoras first put tuning on a (quasi-) scientific basis by discovering the ratios of the first three overtones of the harmonic series:
Octave = 2/1 Fifth = 3/2 Fourth = 4/3 (Click here: Pythagoras: Music and Space for an excellent interactive demo with sound.)
Pythagoras and his followers regarded this 1-2-3 series as holy - the ancient Greek philosophers were fascinated by numbers, believing that certain numbers, and the relationships between those numbers, had divine significance.
The Pythagorean scale was thus constructed using only octaves, perfect fifths and perfect fourths.A perfect fifth (3/2) plus a perfect fourth (4/3)
= (3 x 4)/(2 x 3) = 2, an octave.If C = 1, c (octave) = 2, then:
F = Fourth up from C = 4/3
(Same as fifth down from c.)G = Fifth up from C = 3/2
D = Fourth down from G = 3/2 x 3/4 = 9/8
(Same as up a fifth to D (next octave), down an octave.)A = Fifth up from D = 9/8 x 3/2 = 27/16
E = Fourth down from A = 27/16 x 3/4 =81/64
B = Fifth up from E = 81/64 x 3/2 = 243/128
This gives us the Pythagorean diatonic scale:
C=1; D=9/8; E=81/64; F= 4/3; G=3/2; A=27/16; B=243/128; c=2/1.
(Note that all the numbers in these ratios are divisible either by 3 or by 2.)
Pythagoras himself realised that this system had problems, as twelve pure fifths will not fit into seven octaves:
7 octaves = (2/1) ^7 = 128
12 fifths = (3/2) ^12 = 129.74This discrepancy is known as the "Pythagorean Comma", and two millennia after Pythagoras' death mathematicans, philosophers, churchmen and academics were still arguing about the best way to divide the comma into the other intervals in the scale...
The Pythagorean third, 81/64, is very sharp to the pure third, 5/4. The difference is called the "Syntonic Comma", and again has been the source of much argument through the centuries. But the Pythagoreans held that the holy purity of the numbers was paramount, not the judgement of the human ear. Besides, they didn't use the third much, if at all.
Back to topThe Harmonists
The Greek scholars known as the Harmonists followed in Pythagoras' footsteps through the centuries. The next great Greek in the tuning debate was Aristoxenus (around 450 BCE), who held that the judgement of the ear with regard to intervals was superior to arbitrary mathematical ratios. (As one of his scales was composed of equal tones and equal halves of tones, some 16th century theorists took this to mean that he had invented equal temperament.)
Claudius Ptolemy (the geographer), who lived in the 2nd century CE, documented a bewildering variety of strangely-named scales, as advocated by Pythagoras, Aristoxenus, Eratosthenes, Archytas, and Didymus. And of course he had his own set of scales too - one of these, his "syntonic diatonic", coincides with the later system of Just intonation (based on the first five intervals of the harmonic series - octave, fifth, fourth, major third, minor third) and he is thus sometimes credited as the inventor of that system.
Ptolemy's position was that the best tuning is that for which ear and ratio are in agreement (he took it for granted that agreement was possible...). At the same time he maintained that a tuning was correct only if it used "superparticular ratios", where the fractional numerator exceeds the denominator by 1 - i.e. 2/1, 3/2, 4/3, 5/4, 6/5, 9/8, 10/9, 16/15, etc.
From a modern scientific viewpoint most of these Greek gentlemen seem to have been more concerned with numerology and mysticism than with musical harmony. Nonetheless, Pythagorean and Ptolemaic tuning held sway well into the 13th and 14th centuries. At that time the French Academie at Notre Dame still held that only perfect fifths could be used to construct a scale; the 3 in its ratio 3/2 represented the Holy Trinity and was thus sacrosanct.
Back to topJust Intonation
Theorists had long postulated that musical consonance was the product of simple whole-number ratios. Just intonation is based on the first five intervals of the harmonic series - octave, fifth, fourth, major third and minor third.
Note C D E F G A B c Ratio 1/1 9/8 5/4 4/3 3/2 5/3 15/8 2/1 Cents 0 204 386 498 702 884 1088 1200 C, F and G major triads sound wonderful in this tuning, as all the ratios are pure. But look what happens when we play a D major triad:
Note C D E F G A B c Ratio to C 1/1 9/8 5/4 4/3 3/2 5/3 15/8 2/1 Ratio to D 8/9 1/1 10/9 32/27 4/3 40/27 5/3 16/9 Cents -204 0 182 294 498 680 884 996 The D to A fifth interval is now only 680 cents wide, and that 22 cent difference to pure really makes it howl. No wonder it was known as the "Wolf" fifth.
This is the full chromatic just scale, which incorporates Ptolemy's "superparticular ratios" mentioned above:
Note Interval Ratio (Decimal) Freq. x C root 1 1.000 1.000 minor second 15/16 (0.9375) 1.066 second 9/10 (0.9) 1.112 D major second 8/9 (0.889) 1.125 minor third 5/6 (0.833) 1.200 E major third 4/5 (0.8) 1.250 F fourth 3/4 (0.75) 1.333 G fifth 2/3 (0.667) 1.500 minor sixth 5/8 (0.625) 1.600 A major sixth 3/5 (0.6) 1.666 B seventh 8/15 (0.533) 1.875 c octave 1/2 (0.5) 2.000 This works just beautifully for C, F and G major triads but the moment you play a D or stray into keys like Ab, E, or F# major it sounds like nothing on earth.
Just Intonation NetworkBack to topMeantone Intonation
Just intonation may well have satisfied the superstitions of the church, but more adventurous composers became frustrated by the restrictions it imposed on harmony and modulation. By the 15th century musicians had begun looking for ways to "temper" their instruments to allow use of a greater number of intervals.
One of the true pioneers in the history of temperament was Pietro Aron, who described the meantone temperament in 1523. Meantone intonation is based on the philosophy that way-out-of-tune thirds are more unpleasant than slightly-out-of-tune fifths, so it sacrifices some of the purity of the fifths to bring the thirds into line.
Meantone brought eight of the thirds into line beautifully, but the remaining four - Db - F, F# - A#, Ab - C and B - D# - sounded awful at 427 cents (the pure major third is 386 cents). It also had the bane of the "Wolf Fifth" - all its fifth intervals are around 696.6 cents, a pretty good approximation of the ideal 702 cents figure except for the one black sheep, the Ab - Eb interval, which at 737.7 cents was likened to the sound of a wolf howling, and was to be avoided at all costs.
Meantone restricted composers to a limited selection of key signatures. It gave sweet thirds and fifths in key signatures close to C, but the "distant" keys were way out of tune. It is called meantone because it takes the average, or "mean", on where to place certain pitches. If C and E are tuned as a perfect major third of 386 cents, D should be tuned at 204 cents (9/8) for the key of C, but at 182 cents (10/9) for the key of D. Tuned at 193, D is right in the middle; 193 is the mean between 182 and 204.
Meantone uses a system of "superscripts" to indicate the amount each note in the scale is tempered. This is expressed in fractions of a comma - the "Pythagorean Comma" mentioned above.
In this notation the Pythagorean scale and the diatonic quarter-comma scale (so-called because it tempers the fifth by a quarter of a comma) look like this:
Pythagorean C0 D0 E0 F0 G0 A0 B0 C0 Meantone C0 D-1/2 E-1 F+1/4 G-1/4 A-3/4 B-5/4 C0
Complete 1/4-comma meantone scale
 (Pietro Aron - "Toscanello in Musica", Venice, 1523).
(Pietro Aron - "Toscanello in Musica", Venice, 1523).
Aron's scheme was refined by a myriad of musical theorists and scholars in the following centuries. There are countless different varieties of Meantone intonation, with the comma divided among the rest of the intervals in ever more esoteric ways, but all follow the same basic philosophy.
Despite its drawbacks, meantone was the dominant European keyboard tuning system for over 400 years, from its introduction in the late 15th century until well into the 19th century.
Back to top
Werkmeister - Kirnberger - Thomas Young
Well temper was a further development of Meantone intonation, designed to allow use of all the key signatures. It was pioneered by Andreas Werckmeister (1645 - 1706), among others, in the late 17th century. "Well Temper" tamed the wolf, but left varying degrees of "out-of-tuneness" in the more distant keys. This gave rise to the concept of "key colour" - as different keys are out of tune in differing amounts, and in different places, they have different characters.
(For more on "key colour", click here.)
Opponents of equal temper argue that much is lost when Bach or Mozart is performed in equal temperament, as these composers were well acquainted with the different "key colours", and used them deliberately for effect. "Playing Bach's Well-Tempered Clavier in today's equal temperament is like exhibiting Rembrandt paintings with wax paper taped over them", in the words of one scholar. Mozart's music also gains another dimension when played in its original temperament.
(Equal temperament has no "key colours". As all its intervals are equal, the blend of intervals is the same in every key, so all keys sound alike. "Key colour" is a feature of irregular temperaments like Meantone and Well Temper.)Well temper and equal temper are not the same thing. It is true that Well Temper was often called equal temper when it first came into vogue but this was not because all its intervals were equal, but because it made it all keys equally usable. Each key, however, had a slightly different character: Bach wrote "The Well-Tempered Clavier" in all 24 key signatures to exploit those differences, not because there were no differences.
It is documented that both Bach and Werckmeister were opposed to the rigid mathematical treatment implied by the term "gleichschwebende" - which translates literally as "like-beating". "Like-beating" implies that parallel intervals beat equally in all keys - which is only true of equal temper.
Well temperament was a kind of halfway house between meantone and our modern equal temperament - and came in many flavours. Well temperament has been researched by many music theorists and there are many different schemes. Some keyboard tuners use different schemes depending on what music will be played on the instrument (or customer preference). Here for example are three of the most widely-accepted well-tempered schemes, compared to the equal-tempered scale, with the differences tabulated in cents:
| Note | A | #/b | B | C | #/b | D | #/b | E | F | #/b | G | #/b |
| Equal Temperament | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Werkmeister lll | 0 | +8 | +4 | +12 | +2 | +4 | +6 | +2 | +10 | 0 | +8 | +4 |
| Kirnberger lll | 0 | +6 | -2 | +10 | +1 | +3 | +4 | -3 | +8 | +1 | +7 | +2 |
| Vallotti & Young | 0 | +6 | -4 | +6 | 0 | +2 | +4 | -2 | +8 | -2 | +4 | +2 |
The Well-Tempered Clavier
The most famous "Well Temper" of all time is of course Johann Sebastian Bach's "Das Wohltemperirte Clavier" (The Well-Tempered Clavier) - two sets of preludes and fugues for keyboard, each set consisting of 24 preludes and 24 fugues in all the major and minor keys, the first set dating from 1722, and the second from 1744. The exact temperament that Bach actually used has been a bone of contention among musicologists for over 250 years. This is the DaVinci Code - and the Holy Grail - of the temperament jungle.
"The exact tuning of his instruments as well as of the whole orchestra had his greatest attention. No one could tune and quill his instruments to please him. He did everything himself." (1774, New Bach Reader, #394) Forkel then presented it thus:
"Nobody could install the quill-plectrums of his harpsichord to his satisfaction; he always did it himself. He also tuned both his harpsichord and his clavichord himself, and was so practised in the operation that it never cost him above a quarter of an hour. But then, when he played from his fancy, all the 24 keys were in his power; he did with them what he pleased. He connected the most remote as easily and as naturally together as the nearest; the hearer believed he had only modulated within the compass of a single key. He knew nothing of harshness in modulation; even his transitions in the chromatic style were as soft and flowing as if he had wholly confined himself to the diatonic scale. His Chromatic Fantasy, which is now published, may prove what I here state. All his extempore fantasies are said to have been of a similar description, but frequently even much more free, brilliant, and expressive." (1802, New Bach Reader, p436. English translation by Kollmann, 1820.) (CPE Bach and Forkel quotes borrowed from www.larips.com, with thanks.) Unfortunately neither Bach nor his sons ever saw fit to write down explicit instructions on how to tune this temperament, and it has thus sadly been lost to us for almost 250 years. However, according to Dr. Bradley Lehman, A.Mus.D. (harpsichord), of Goshen College, Indiana, the key to the mystery has been hidden in plain sight since 1722 - in Bach's own hand, on the title page of the original manuscript of "Das Wohltemperirte Clavier". Dr. Lehman's intimate knowledge of Bach's music, and extensive hands-on experience of harpsichord tuning, enabled him to crack the code at last. His breakthrough came in April 2004 and is making huge waves internationally in the world of the harpsichord and the pipe organ. A number of newly-built pipe organs using Lehman's "New" Bach Temperament have already been installed in music colleges and churches by one of America's leading organ builders, and work is in hand on more instruments. A newly-built "Bach/Lehman" organ was recently dedicated in Laajasalo Church in Helsinki, Finland. Harpsichord concerts in this temperament are being performed around the world. For further information, see:
Dr. Lehman's fascinating website. Back to top
Fretted Instruments
There is little question but that the majority of fretted instrument makers and players had adopted equal temperament - or as close an approximation to it as they could achieve - by the 16th century. Nicola Vicentino wrote in 1555 about the difficulties arising from the parallel usage of two systems - meantone for keyboard instruments, and equal temperament for the fretted instruments. ("L'antica musica ridotta alla moderna prattica", Rome, 1555.) Orchestras of the period became quite large, to compensate for the fact that their different sections could not all play at the same time.
Alongside Pietro Aron, two other major contributors to the tempering revolution of the 16th century were Gioseffo Zarlino and Francisco Salinas. While both Zarlino and Salinas propounded similar irregular tunings for keyboards, both men also recognised the necessity for equal temperament on fretted instruments. Indeed Salinas, a blind professor of music in Naples, gave the first precise mathematical definition of equal temperament when in 1577 he wrote:
"We judge this one thing must be observed by makers of viols, so that the placing of the frets may be made regular, namely that the octave must be divided into twelve equal parts equally proportional, which twelve will be the equal semitones." (De musica libri VIII, Salamanca, 1577.)
Vincenzo Galilei
Before the 16th century, very little was known about the generation and transmission of sound. The first scientifically valid experiments were made by Vincenzo Galilei (1520 -1591), a professional musician, lutenist, composer, theorist, and teacher - and father of Galileo Galilei (1564 - 1642). Using much the same methodology as Pythagoras (suspending weights from strings), he gathered data which enabled him to establish the relationship between pitch and frequency, and state the laws of harmony and dissonance, essentially as they are understood today. He also demonstrated that the natural frequency of a vibrating string is dependent on its length, weight, and tension.
Musicians had undoubtedly become quite skilled in the art of adjusting their frets (which in instruments of the time usually consisted of lengths of gut, tied around the neck) by trial and error, or by simple geometrical methods. But the first appearance in writing of a practical approximation for placing frets in equal temperament - the 18:17 ratio, or "Rule of 18" - was given by Vincenzo Galilei in his "Dialogo della musica antica e moderna", published in Florence in 1581.
Galilei explained the need for equal semitones logically and correctly - since the frets are placed straight across the six strings, the order of diatonic and chromatic semitones is the same on all strings. In chords, therefore, a C# might be sounded on one string, and a Db on another - this will be a very false octave unless the instrument is in equal temperament.
The Rule of 18
The "Rule of 18" puts the first fret at 1/18th of the distance from the nut to the bridge, the second fret at 1/18th of the distance from the first fret to the bridge, and so on. This system made it simple to mark out a fret scale on a piece of wood using just a ruler and a compass, and it remained the basis of practical fretboard construction for over 300 years.
The Rule of 18 results (theoretically) in intervals of 99 cents:
| Notes | E | F | F# | G | Ab | A | Bb | B | C | C# | D | Eb | E |
| Cents | 0 | 99 | 198 | 297 | 396 | 495 | 594 | 693 | 792 | 891 | 990 | 1089 | 1188 |
This almost certainly gave acceptable intonation with the natural gut strings of the period, which were far more elastic than modern-day steel or nylon strings. The instruments of the day seldom had more than 8 or 9 frets to the body, so a minor adjustment to the string length at the bridge would suffice to tame any tendency to "out-of-tuneness" up the neck.
Back to top
The emerging technology of the 1800's had a profound impact on keyboard tuning. The issue was forced by advances in piano design. In the search for more power, high-tension, cast-iron-framed pianos, using newly-developed, much stronger wire, came into use. As the tension increased, so did the number of audible overtones. Dissonances that could be tolerated on the much more lightly strung harpsichords and fortepianos became unbearable on the new high-tension instruments. Musicians and composers - the Romantics in particular - wanted a temperament that would let them modulate freely without encountering the wolf. The first pianos to be tuned to equal temperament were produced by Broadwoods in the middle of the 19th century.
The 19th century was a time of tremendous advances in materials technology and engineering. Science was becoming synonymous with progress in all walks of life, and musical instrument design was not immune to its inroads. The "mathematically correct" equal temperament held great appeal in this atmosphere of trust in science, particularly since vast improvements in the accuracy and sophistication of machine tools were making it possible to mass-produce musical instruments to a degree of precision undreamed of a few generations earlier.
Equal temperament is the ultimate compromise. Tonal purity is sacrificed for freedom of modulation. Depending on your viewpoint, equal temperament either a) makes every key equally in tune, or b) makes every key equally out of tune... The idea is to make it possible to play all intervals and chords, in all keys, with the same relative accuracy. Although every key is very slightly out of tune, every key is also useable. No key sounds worse than any other key. The same applies to all chords.
The final countdown The key to the equal tempered scale is the number 1.0594631, the twelfth root of two. This number has a bunch of tricks up its sleeve! If you multiply one by it twelve times you get two (and if you divide two by it twelve times you get one...).1 x 1.0594631 = 1.0594631
1.0594631 x 1.0594631 = 1.1224621
1.1224621 x 1.0594631 = 1.1892071
1.1892071 x 1.0594631 = 1.2599211
1.2599211 x 1.0594631 = 1.3348399
1.3348399 x 1.0594631 = 1.4142136
1.4142136 x 1.0594631 = 1.4983071
1.4983071 x 1.0594631 = 1.5874011
1.5874011 x 1.0594631 = 1.6817929
1.6817929 x 1.0594631 = 1.7817975
1.7817975 x 1.0594631 = 1.8877487
1.8877487 x 1.0594631 = 2.0000001
The right-hand column of figures defines the semitones of the equal tempered scale, which gives us 12 semitones of 100 cents each and thus an octave of exactly 1200 cents. The old Rule of 18 was not so far off - extrapolation of the twelfth root of two ratio gives us a divisor of 17.817152.
The equal-tempered fifth is fairly "sweet" at 700 cents compared to the just fifth at 702 cents, and the equal-tempered fourth works well at 500 cents compared to 498 cents for the just fourth - but thirds, sixths and sevenths fare less well. Thirds are especially troublesome, as the equal-tempered minor third is 16 cents flat to the just minor third, and the equal-tempered major third is 14 cents sharp of just. The equal-tempered major sixth is 16 cents sharp of just, and the equal tempered major seventh is 12 cents sharp of just. The only interval which is identical in the two scales is the octave.
© Paul Guy 1999 - 2006
![]()
Links: