Åter till "Handbok"
VARFÖR STÄMMER DEN INTE?av Paul Guy
© Paul Guy 1990-2006
Ett av de vanligaste problemen jag stöter på som gitarreparatör är kunden som är övertygad om att hans instrument "inte stämmer". Detta trots ibland upprepade besök till olika reparatörer för att få gitarren intonerad eller justerad.
De flesta moderna elgitarrer kan intoneras att stämma mycket bra och även de flesta moderna akustiska gitarrer med icke-justerbara stall stämmer förhållandevis bra. Förutsatt att (a) stallet sitter på exakt rätt plats (och i mån av justeringsmöjlighet, är intonerad för de strängar som sitter på) och (b) att sadeln, strängarna och stämskruvarna är i gott skick och gitarren är väljusterad i övrigt, finns det inte mycket mer som inverkar på stämningen. (Det är ytterst sällsynt att stämnings-problem orsakas av felplacerade bandstavar. Banden brukar sitta rätt även på de billigaste gitarrer.)
Trots detta finns det många gitarrister som kämpar förtvivlat för att få sina gitarrer att stämma - eller är på evigt jakt efter ett instrument som "stämmer i banden". De lider, bl a, av att instrumentet stämmer acceptabelt i vissa tonarter, men låter helt ostämd i andra: av att aldrig kunna få fler än ett öppet ackord att stämma acceptabelt: av att aldrig kunna få vissa barré ackord och intervaller att stämma: och av tjatet från bandkamraterna.
Problemet ligger oftast i ett missförstånd. I likhet med de allra flesta bandade instrument är gitarrens band placerade för att återge liksvävande intervaller (eng: "Equal Temperament", tyska "Gleichschwebende Temperatur"") Därför måste den också stämmas till liksvävande intervaller. De allra flesta som har de beskrivna stämningsproblemen försöker stämma sina gitarrer till rena (eng: Just) intervaller. Detta fungerar inte på en gitarr - hur noggrant justerad den än är. Bandens placeringar är uträknade enligt den liksvävande temperaturen, som har även varit i praktiskt taget universellt bruk på klaviaturinstrument i över 150 år.
Det liksvävande temperaturens stora fördel över tidigare system, är att det gör det möjligt att spela alla intervaller och ackord, i alla tonarter, med samma relativa exakthet. Medan varje tonart är aningens ostämd, går det bra att spela i alla tonarter. Ingen låter mer ostämd än någon annan. Detsamma gäller alla ackord. Teoretiskt sett, vill säga. I praktiken finns vissa intervaller och ackord som fortfarande låter dissonanta. Syftet med denna artikel är att förklara hur man får det bästa ur systemet.
Det finns betydliga skillnader mellan den rena skalan och den liksvävande - de enda intervaller som är exakt samma i båda skalorna är oktaverna. Det säger sig självt att det inte går att stämma ett instrument efter en skala som den inte var konstruerad för och vänta sig att resultatet blir tillfredsställande. Därför är det viktigt att lära sig principerna bakom liksvävande stämning - de är i praktiken ganska enkla. Vi börjar från början, med lite bakgrund.
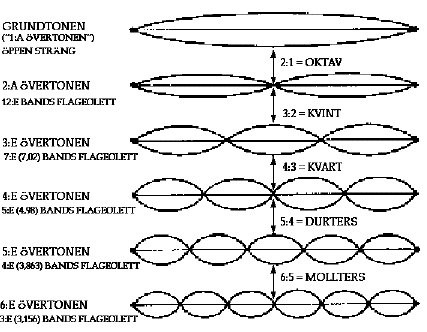
DEN NATURLIGA TONRADEN
Den naturliga tonraden är samma sak som den naturliga övertonsserien hos vibrerande strängar. Grundtonen ("första övertonen") är frekvensen hos hela strängen. Andra övertonen (oktaven) är hälften av stränglängden. Tredje övertonen (kvinten) är två tredjedelar av stränglängden. Fjärde övertonen (kvarten) är tre fjärdedelar av stränglängden och femte övertonen (tersen) fyra femtedelar av stränglängden, o s v. Gitarrister känner igen dessa heltalsdelningar av stränglängden som flageolettoner.
Man började undersöka de matematiska relationerna mellan skaltonerna i det antika Grekland, där det spelades flitigt på lyra och kithara. Dessa instrument var stämda efter en sextonig diatonisk skala. Terpander, en grekisk matematiker, räknade ut denna skala år 650 f.Kr., men det var gamle Pytagoras som, medan han undersökte de fysikaliska egenskaperna hos vibrerande strängar, först försökte räkna ut de matematiska relationerna i den skala vi idag kallar för C-dur skalan - år 550 f.Kr! Enligt Pytagoras har tonerna i en C-dur skala följande förhållanden till grundtonen:
C=1; D=8/9; E=64/81; F=3/4; G=2/3; A=16/27; H =128/243; c =1/2.
Vid närmare granskning visade det sig dock att det finns felaktigheter i Pytagoras' skala (beroende åtminstone delvis på, antagligen, att de strängar och mätverktyg han hade att arbeta med inte var särskilt exakta). Bland annat borde tolv kvinter vara detsamma som sju oktaver enligt Pytagoras, men hans matematik stämmer inte på den punkten - det s k "Pytagoreiska Kommat". Denna skillnad är emellertid så pass liten som 1/9490 eller drygt 0,0005. Däremot är skillnaden mellan den rena tersen 4/5 och Pytagoras' 64/81 (det s k Syntoniska kommat) så mycket som 4/405 - nästan 1%. Och det finns fler skillnader. Dessa skillnader gav upphov till problem med harmoni i polyfonisk musik.
I två sekler rasade debatten bland de lärde om musik såsom det upplevs av det mänskliga örat, kontra musik som ett matematiskt fenomen. Matematiker, filosofer, politiker och t o m kyrkan blandade sig i - oftast helt i onödan. Pytagoras' system fick mycket kritik redan från början, men många "auktoriteter" klängde sig fast vid det ännu en bit in på 1500-talet.
Denna akademiska diskussion gav upphov till många försök att fastställa en matematisk beskrivning av den renstämda, eller "naturliga", skalan. De flesta enades kring en utveckling och korrigering av det Pytagoreiska systemet. Denna skala har följande relationer:
Tabell 1
- Grundtonsfrekvens x
C grundton 1 1,000
liten sekund 15/16 (0,9375) 1,066
sekund 9/10 (0,9) 1,112
D stor sekund 8/9 (0,889) 1,125
liten ters 5/6 (0,833) 1,2
E stor ters 4/5 (0,8) 1,25
F kvart 3/4 (0,75) 1,333
G kvint 2/3 (0,667) 1,5
liten sext 5/8 (0,625) 1,6
A stor sext 3/5 (0,6) 1,666
H septim 8/15 (0,533) 1,875
c oktav 1/2 (0,5) 2,000Detta fungerade skapligt så länge musiker och kompositörer höll sig till modal - diatonisk - harmoni (dvs fram till 1400-talet), men när man började använda kromatiska toner och tonarter alltmer på 1500-talet, blev det verkligen kris. Instrument kalibrerade till "naturliga" intervaller lät förfärligt ostämda när man spelade vissa kromatiska intervaller och i vissa tonarter.
Man försökte med en kompromiss - två satser kromatiska toner (för dur och moll). Många personligheter bidrog till denna kompromiss, men det var nog Gioseffo Zarlino's avhandling "Institutioni Harmoniche" (1558) som gjorde mest för att få de renstämda dur- och mollskalorna allmänt accepterade. I detta system (Figur 2) är C# och Db (och D# och Eb, o s v) två skilda toner - C# är lite lägre än Db. (I liksvävande temperatur är C# och Db bara olika namn för samma ton.)
Tabell 2
Sänkta toner Höjda toner
C 1,000 C 1,000
Db 1,067 C# 1,055
D 1,125 D 1,125
Eb 1,200 D# 1,172
E 1,250 E 1,250
F 1,333 F 1,333
Gb 1,422 F# 1,406
G 1,500 G 1,500
Ab 1,600 G# 1,562
A 1,667 A 1,667
B 1,777 A# 1,757
H 1,875 H 1,875
c 2,000 c 2,000Om man fortsätter med dessa "renstämda" skalor över flera oktaver visar det sig dock att t.ex. tolv kvinter "staplade på" varandra, vilket borde ge sju oktaver, ger en ton 24 cent (cent = hundradel av en halvton) högre. En rad kvarter hamnar 24 cent under oktaven. En rad av terser ligger hela 42 cent från oktaven, och en rad av små terser 64 cent. Eftersom oktaverna måste stämma, innebär det att de olika intervallen inom oktaven måste justeras, med det olyckliga resultatet att intervallen blir olika stora i olika oktaver! Vilket kan ge upphov till kakafoni i flerstämmig musik...
Så för musikerna - och särskilt för instrumentmakarna - var sålunda inte problemet löst. Det går t ex inte att tillverka mekaniska klaviaturinstrument med tolv tangenter per oktav som stämmer enligt två olika skalor. Man gjorde klaviaturer med två uppsättningar "svarta tangenter" för att komma runt problemet, men skapade bara ett ännu värre problem - instrumenten blev i det närmast omöjliga att spela på. För att förenkla instrumenten och samtidigt få harmoni i alla tonarter, var det nödvändigt att hitta på ett bättre system.
DEN LIKSVÄVANDE TEMPERATUREN
Den liksvävande temperaturen hade sina förespråkare redan på 1500-talet. En av dessa, Ramos de Pareja, tros ha hämtat idén från de spanska gitarristerna, som brukade utrusta sina instrument med flyttbara band - av senor, knutna runt halsen - som de placerade i jämna halvtonsintervaller. Men det dröjde ändå in på 1800-talet innan den liksvävande temperaturen som vi använder idag blev allmänt accepterad.Den liksvävande temperaturen jämnar ut - "tempererar" - avvikelserna i de renstämda skalorna genom att göra alla halvtoner "likvärdiga". Därigenom får vi en kompromiss som gör det möjligt att spela alla intervaller i alla tonarter med samma relativa exakthet. Skillnaderna mellan den naturliga tonraden, de renstämda skalorna och liksvävande temperatur framgår tydligt av figur 3.
Tabell 3
SKALORNA JÄMFÖRDANaturliga tonraden Harmoniska & liksvävande
- Sänkta Höjda Liksvävande
C rot 1 1.000 C 1.000 C 1.000 1.0000
m2 15/16 (0.9375) 1.066 Db 1.067 C# 1.055 1.0595
2 9/10 (0.9) 1.112
D (M)2 8/9 (0.889) 1.125 D 1.125 D 1.125 1.1225
m3 5/6 (0.833) 1.2 Eb 1.200 D# 1.172 1.1892
E (M)3 4/5 (0.8) 1.25 E 1.250 E 1.250 1.2599
F 4 3/4 (0.75) 1.333 F 1.333 F 1.333 1.3348
- Gb 1.422 F# 1.406 1.4142
G 5 2/3 (0.667) 1.5 G 1.500 G 1.500 1.4983
m6 5/8 (0.625) 1.6 Ab 1.600 G# 1.562 1.5874
A (M)6 3/5 (0.6) 1.666 A 1.667 A 1.667 1.6818
- Bb 1.777 A# 1.757 1.7818
B 7 8/15 (0.533) 1.875 B 1.875 B 1.875 1.8877
c oktav 1/2 (0.5) 2.00 c 2.000 c 2.000 2.0000Nyckeln till den liksvävande temperaturen är siffran 1,0594631, den tolfte roten av två. Den siffran kan konster, den! Om man mutiplicerar ett med den tolv gånger blir resultatet två (och om man delar två med den tolv gånger blir resultatet ett... ).
Tabell 4
- 1 x 1,0594631 = 1,0594631
1,0594631 x 1,0594631 = 1,1224621
1,1224621 x 1,0594631 = 1,1892071
1,1892071 x 1,0594631 = 1,2599211
1,2599211 x 1,0594631 = 1,3348399
1,3348399 x 1,0594631 = 1,4142136
1,4142136 x 1,0594631 = 1,4983071
1,4983071 x 1,0594631 = 1,5874011
1,5874011 x 1,0594631 = 1,6817929
1,6817929 x 1,0594631 = 1,7817975
1,7817975 x 1,0594631 = 1,8877487
1,8877487 x 1,0594631 = 2,0000001(Jämför dessa siffror med den liksvävande skalan i Fig 3.)
Det skulle gå att skriva en hel bok enbart om de olika skalsystem som finns och har funnits i västerländsk musik. Detta är bara en kort och ofullständig redogörelse av ämnet. Men eftersom praktiskt taget alla gitarrer är konstruerade enligt de principer som jag har förklarat här, blir andra system endast av akademiskt intresse för gitarristen. Jag har bara tagit med det som i mitt tycke är det väsentligaste - och har också förenklat vissa begrepp. Detta är tänkt som en praktisk handledning för gitarrister och inte som en vetenskaplig avhandling.
BANDPLACERING
Siffran 1,0594631, den tolfte roten av två, är även nyckeln till delningen av en greppbräda i "likvärdiga" halvtoner. På gitarren fungerar det så att avståndet sadel - stall (mensuren) och avståndet första band - stall har relationen 1,0594631 : 1. Likaså har avståndet första band - stall och avståndet andra band - stall samma relation, o s v. Detta är ett ganska invecklat sätt att räkna ut bandplaceringen. Vi jonglerar lite med siffrorna så att det blir enklare (se figur 5).Tabell 5
M = mensur (= avstånd sadel - stall)
X = avståndet sadel - 1:a band
M - X = avståndet stall - 1:a band
(M - X)/M = 1/1,0594631
M = 1,0594631 (M -X)
M (1,0594631 - 1) = X (1,0594631)
M / X = 1,0594631/0,0594631
M / X = 17,817152Siffran 17,817 är mycket lättare att handskas med när vi ska dela en gitarrgreppbräda i halvtoner. Man delar bara hela längden (mensuren) med 17,817 och resultatet blir avståndet sadeln - första bandet. Den kvarvarande delen av strängen (mensuren minus första band) delas också med 17,817 för att få avståndet första - andra bandet, och denna procedur upprepas lika många gånger som antalet band. I praktiken är denna metod mycket exakt, för man får 12:e band precis vid halva mensuren och 24:e bandet precis vid tre fjärdedelar av mensuren, vilket ger rena oktaver.
Att sedan alla strängarna, när gitarrren intoneras, blir lite längre än den teoretiska mensuren, är ett fenomen som orsakas av att spänningen på strängen - och därmed tonhöjden - ökar när man trycker ner strängen på banden. Desto tjockare sträng, desto mer ökar spänningen och därför behöver de lägre strängarna mer "kompensation", som denna lilla längdökning kallas. (Se "Intonering" och "Sträckstämning".)
De flesta moderna elgitarrer har en separat, justerbar stallsadel för varje sträng och kan intoneras mycket exakt. Stålsträngade akustiska gitarrer brukar ha en vinklad, rak stallsadel som i de flesta fall ger en tillfredsställande kompensering. De flesta nylonsträngade gitarrer har en rak sadel med samma kompensering för alla sex strängar och detta brukar fungera bra. (Tack vare de mindre skillander i diametrarna hos nylon strängar.)
Figur 6 är en tabell över bandplaceringen på en Fender Stratocaster, uträknad efter "17,817 metoden" som beskrevs ovan. Observera att 12:e bandet ligger precis vid mittpunkten, och att 24:e bandet ligger precis vid halva avståndet 12:e bandet - stallet. Visserligen har en standard (vintage) Strata bara 21 band, men man brukar räkna ut bandplaceringen för 24 band för att få en dubbellkoll.
Tabell 6
Fender Stratocaster - mensur 25,5 tum eller 647,7 mm.
Band Intervall Från sadel Resterande
1 36,3526 36,3526 611,3474
2 34,3123 70,6649 577,0351
3 32,3865 103,0514 544,6486
4 30,5688 133,6202 514,0798
5 28,8531 162,4733 485,2267
6 27,2337 189,707 457,993
7 25,7052 215,4122 432,2878
8 24,2625 239,6747 408,0253
9 22,9007 262,5754 385,1246
10 21,6154 284,1908 363,5092
11 20,4022 304,593 343,107
12 19,257 323,85 323,85
13 18,1763 342,0263 305,6737
14 17,1562 359,1825 288,5175
15 16,1932 375,3757 272,3243
16 15,2843 390,66 257,04
17 14,4266 405,0866 242,6134
18 13,6168 418,7034 228,9966
19 12,8526 431,556 216,144
20 12,1312 443,6872 204,0128
21 11,4504 455,1376 192,5624
22 10,8077 465,9453 181,7547
23 10,2011 476,1464 171,5536
24 9,6286 485,775 161,925
Referenser:
Sir Jack Westrup & F. Ll. Harrison: Collins Encyclopedia of Music, London 1984
Franz Jahnel: Manual of Guitar Technology, Frankfurt 1981
Hideo Kamimoto: Complete Guitar Repair, New York 1975
R. F. Goldman: Harmony in Western Music, London 1965
Gilbert Chase: The Music of Spain, New York 1959
Sir James Jeans: Science and Music, Cambridge 1937
© Paul Guy 1990-2006
Delar av denna text ingår i "Stämma Gitarren" av Paul Guy
CG6751, AB Gehrmans Musikförlag ©1990